IHH Engineering

Knowledge

Finite Elemente Methode

Die FE Methode ist ein numerisches Verfahren zur Lösung von Systemen von (partiellen) Differentialgleichungen. Speziell für Aufgaben der Elastomechanik ist für ein Gebiet G (Körper) die Grundgleichung der Elastomechanik:

Grundgleichung für das Verschiebungsfeld:

Grundgleichung für das Spannungsfeld:

\begin{matrix} Δ u + \frac{1}{1 - 2 ν} \nabla (\nabla \cdot u) = 0 \\ Δ σ + \frac{1}{1 + ν} Δ \bar{σ} = 0 \\ \bar{σ} = σ_{x} + σ_{y} + σ_{z} \end{matrix}

Die Lösung dieser Differantialgleichungen geschieht bei der FEM mittels der mathematischen Methoden der Variationsrechnung und geht auf das Verfahren von Ritz zurück. Als Funktional dient das Minimum der potenziellen Energie (Toricelli, Euler, Leibniz), welches besagt, dass sich ein (elastischer) Körper unter dem Einfluss äußerer Kräfte immer so verformt, dass die dadurch in ihm gespeicherte Verformungsenergie (=potenzielle Energie) den kleinsten Wert einnimmt. Für elastomechanische Probleme kann die totale potenzielle Energie eines dreidimensionalen isotropen Körpers wie folgt beschrieben werden:

Π = \frac{1}{2} \underset{V}{∭} σ^{T} (ε - ε (ϑ)) dV - \underset{V}{∭} p^{T} f dV - \iint_{S} q^{T} f dS - \sum_{i = 1}^{m} F_{i}^{T} f_{i}

Der betrachtete Körper (Gebiet) wird nun durch einfache gleichartige Teilgeometrien angenähert bzw. aufgeteilt. Diese Elemente (Teilgebiete) sind die finiten Elemente. Zweidimensionale Gebiete werden in Dreiecke oder Parallelogramme aufgeteilt. Dreidimensiale Gebiete (Körper) in Tetraeder oder Quader.

Dieser Schritt wird allgemein als Vernetzung bezeichnet, die diskretisierte Geometrie Finite-Elemente Netz. Es deutet sich an, dass für eine genauere Approximation des betrachteten Gebietes, die Elemente kleiner gewählt werden müssen, zumindest dort wo eine genauere Approximation gewünscht wird.

Fachwerk / Rahmenstruktur

Für Systeme die aus stab- oder balkenförmigen Teilelementen aufgebaut sind, wie Fachwerke oder Rahmenstrukturen, ist die Aufteilung in finite Elemente (Vernetzung) dahingehend einfacher, als diese Systeme die Elementegrundstruktur bereits vorgeben.

Diese Aufteilung in gleichartige Elemente gestattet es nun, die mathematischen Beschreibungen einheitlich für die einzelnen Elemente darzustellen, so dass mit Hilfe mathematischer Methoden die numerische Behandlung einer beliebigen Anzahl solcher zusammenhängender Elemente als Ersatz für den betrachteten Körper möglich wird. Dies geschieht nun auf der Basis der Variationsrechnung wie folgt:

I. Die Verformungsenergie wird für einen Elementtyp berechnet, indem ein Ansatz für eine Verschiebungsfunktion in der Form u(x) für eindimensionale Elemente (Stäbe, Balken) bzw. u(x,y) für 2 dimensionale Elemente (Scheiben, Platten) in den Formen gemacht wird

\begin{matrix} u (x) = \sum_{i} c_{i} x^{i} \\ u (x, y) = \sum_{i} \sum_{j} c_{i}_{j} x^{i} x^{j} \end{matrix}

In jedem Element treten dabei die zu bestimmenden Koeffizienten c_i bzw. c_ij auf.

II. Um diese Koeffizienten zu bestimmen benutzt man die oben angegebene Beziehung für die potenzielle Energie als Funktional einer Variationsaufgabe. Um das physikalische Prinzip des Minimums der potenziellen Energie auszunutzen, sind diese Koeffizienten also genau so festzulegen, dass der Energieausdruck minimal wird.

Setzt man bespielsweise die elastizitätstheoretischen Beziehungen für die Verformungen eines Balkenelmentes an, erhält man für die potenzielle Energie in Abhängigkeit der Verschiebung u(x)

Π_{B} = \frac{1}{2} \int_{0}^{l} u'' {(x)}^{2} dx - \int_{0}^{l} q (x) u (x) dx - \sum_{i = 1}^{n} F_{i} w_{i} - \sum_{j = 1}^{m} M_{i} w_{i}'

Dieser Ausdruck wird in der Literatur auch als Formänderungsenergie beschrieben. Die Ansatzfunktionen müssen dabei vorallem die Übergangsbedingungen von einem Element zum anderen erfüllen, beispielsweise dass die Biegeverformung einen stetigen Übergang von einem zum nächsten Element erfüllt (konforme Elemente). Für das mathematische Zusammenfügen der Elemente ist es offensichtlich, dass dies schematisch nur möglich ist, wenn alle Elemente gleich behandelt werden können unabhängig von ihrer Größe. Dazu werden die Elemente auf ein Einheitselement abgebildet, z.B. wird die Balkenlänge auf die dimensionslose Variable ξ = x/l umgerechnet und als Koeffizienten werden die Verschiebungen in den Elementknoten verwendet. Der Verschiebungsansatz für ein Element wird dazu als Linearkombination dieser Verschiebekoeffizienten mit Ansatzfunktionen umgestellt:

u_{E} (x) = \sum_{i = 1}^{p} u_{i} N_{i} (x)

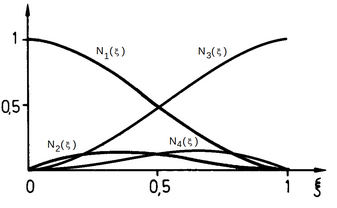
p ist dabei die Anzahl der Knotenpunkte in einem Element. Diese Formfunktionen müssen nun wegen ihrer Interpolationseigenschaft die Bedingung erfüllen, dass sie in dem Knotenpunkt mit der Verschiebung u_i den Wert 1 annimmt und in allen anderen Knotenpunkten 0 wird. Für eine Biegebalkenelement müssen beispielsweise in jedem Knoten die Verschiebung u sowie der Biegewinkel u' bestimmt werden, für 2 Knoten also u₁, u₁', u₂, u₂'. Daraus ergeben sich 4 Ansatzfunktionen, die folgende prinzipielle Form haben müssen:

III. Die Beiträge der Formänderungsenergien jedes einzelnen Elementes können nun aufgetsellt werden, um die Energie für das gesamte System aufzustellen müssen diese Beiträge aufsummiert werden. Um dies für eine beliebige Anzahl von Elementen zu erreichen wird sinnvollerweise die Matrizenrechnung angewendet. Hierzu werden alle Knotenverschiebungen untereinander in einem Spaltenvektor u dargestellt. Am Ende erhält man die Formänderungsenergie in Matrizenschreibweise:

Π_{FE} = \frac{1}{2} u^{T} S u + d^{T} u

Der Vektor u beinhaltet die beschriebenen Knotenvariablen. S ist die symmetrische Steifigkeitsmatrix und d der Koeffizientenvektor. Die Bedingung des stationärwerdens der Formänderungsenergie führt auf das lineare Gleichungssystem:

S u + d = 0

Randbedingungen können derart berücksichtigt werden, indem Spalten und Zeilen der Steifigkeitsmatrix S null gesetzt werden, die den Knotenvariablen entsprechen. Die Lösung des Gleichungssystems ergibt direkt die Werte u in den Knoten. Über die Formfunktionen können Zwischenwerte ermittelt werden.